Game theory is a framework that helps to make decisions in situations where two or more players compete. Game theory is used in a wide variety of fields, including business, finance, economics, political science, and psychology (Harrington, 2015). The present paper provides five examples of how game theory explained my and my friends’ decisions in real life. In particular, the paper explains my behavior when I was caught trying to conceal the fact that I wasted my parents’ money and my decision-making process when buying my first car. I also try using the game theory to explain why men should always apologize and solve the hang-up problem. I also demonstrate how game theory explained the pricing strategy of the bakery I work in. In this paper, I try to analyze every situation from different sides to explain how the assumptions may change the selected strategy of all players.
Example 1: Childhood Lies
Looking back at my childhood, I realize that I was forced to solve the world-famous prisoner’s dilemma twice after being caught for spending money I was not supposed to spend. When I was around 10, my mother asked my cousin and me to go to the grocery store to buy a small list of products. After buying everything, my cousin and I realized that we wanted ice cream, so we decided to spend some change on ice cream. After eating the treat, a realization that mother would be infuriated dawned on us. We came up with a story that we lost all the change while walking back. As we came back home, my mother said that everything was OK and we should not feel sorry about losing the money. However, my uncle felt that there was something wrong with our story and took us to different rooms to interrogate us separately. My uncle told me that if he gets to know that I was lying, I will be punished for three weeks without TV. However, if I confessed, I would have o stay only one week without TV. I assumed that the same deal was with my cousin.
This situation can be analyzed using game theory. The payoff matrix for this game is demonstrated in Table 1 below.
This game is not solvable using a dominant strategy. However, it can easily be solved using the expected value (EV) of each choice. Since we had no idea how the other person would act, the probability of lying or confessing was 50% for both actions. Thus, including the probabilities in the equation is not required. The EV of confessing for both my cousin and me would be -2, while the EV of lying would be -3. Since the EV of confessing is higher than that of lying, we should have both selected confessing to stay without TV for one week.
In reality, I stayed faithful to the lie, as I was loyal to my cousin, while my cousin was rational and told the truth. I felt angry for being betrayed and decided that I will never trust my cousin ever again.
As luck would have it, about six months later, a similar situation occurred, with the only exception that this time it was not ice cream but Coca-Cola. We always loved Coke, even though my father said it was unhealthy. As we were taken to different rooms once again, I was determined to tell everything to my father, who was interrogating us this time. If we turn this into math, the probability of my cousin confessing to my father was 95%. What I did not realize at that point is that my cousin thought that I remained faithful to him and I would lie to my father. I would estimate that he believed that I would lie with a probability of 80%.
This game can be solved using a mixed strategy. The probability that would make a person randomize their decision would be the same in this situation, as the benefits are similar:
-1p – 1 (1-p) = -3p + 0 (1-p)
– p – 1 + p = -3p
3p = 1
p=1/3
In order to come up with a rational decision, I needed to compare the perceived probability of my cousin betraying me with the 33.3%. Since I believed that the probability of my cousin selling me out was 95%, I made a rational choice to betray my cousin. At the same time, my cousin also made an absolutely rational decision, as he believed that I would lie with an 80% chance, which was above the 33.3% threshold.
While the application of the game theory made sense for the second situation, it did not make sense for the first situation. Looking back at these events, I understand that there was a lot more to selecting between the punishments for me. I always was a person of principles, and my central principle was never to betray. Thus, by telling on my cousin would punish myself for being no loyal to my principles. If we quantify the damage to my moral integrity as one week without TV and reward for following my principle minus two weeks without TV, my decision made more sense. The Reward matrix would look like Table 2 below.
This game can be solved using a dominant strategy. In this game, I am always better off lying, as both outcomes were better for me regardless of what my cousin does. However, since my cousin did not have a dominant strategy, he made a rational choice to confess, as the EV of this choice was higher. It is also crucial to notice that I abandoned my principle of never betraying after the situation. Therefore, the analysis of the second game remains relevant.
Example 2: Men Should Always Apologize
Throughout my life, I heard a joke from male stand-up comedians that sounded like this:
“My girlfriend and I live in perfect harmony. We have no problems with fights, as they always follow the same scenario. If I am at fault, my girlfriend gets mad, and I apologize. If my girlfriend is at fault, she gets mad, and I apologize.”
This joke and the attitudes of people around me made me believe that men should always apologize regardless of whose fault it is. This idea can be proved using game theory. Before setting up a game, it is necessary to make some assumptions. First, we are talking about small- and medium-scale fights that do not include a major problem, like cheating, beating, or abusing the partner in any way. Second, the criteria for selecting the strategy are damage/benefits gained for the ego and not to the relationship. Third, there are only two possible strategies in the fight, apologizing or waiting for an apology. Finally, we assume that benefits for the
The payoff matrix for boyfriend and girlfriend would look like the one demonstrated in Table 3 below.
This game is not solvable using a dominant strategy, which implies that a mixed strategy should be used. At this point, it is crucial to understand that the probability of the girlfriend apologizing and the boyfriend apologizing is not the same. The choice of the strategy will depend upon the perceived probability that the other person will apologize. In this game, the probability that would make a person randomize their decision would be the same, as the benefits are similar. It can be found using the following calculations.
2p – 4 (1-p) = 4p – 5 (1-p)
2p – 4 + 4p = 4p – 5 +5p
-2p + 4p – 5p = -5+4
-3p = -1
p = 1/3
In other words, both boyfriend and girlfriend should randomize their decision only if the probability of the other person apologizing is below 33.3%. This can be confirmed by calculating the EV of apologizing and waiting for the apology for both players. Let’s suppose that the probability of the girlfriend apologizing is 60%. Then, the EVs for the boyfriend’s decisions are the following:
EV (apologizing) = 2*0.6 – 4*0.4 = 1.2 -1.6 = -0.4
EV (waiting) = 4*0.6 – 5*0.4 = 2.4 – 2=0.4
Since the EV of apologizing is lower than the EV of waiting, the boyfriend should choose to wait.
This explanation is a more-or-less accurate representation of what happens in real life. Boyfriends and girlfriends misjudge the chances of their significant other apologizing. Thus, the game often leads to both players waiting for an apology, which leads to the most unsatisfactory result for both.
While these findings are crucial, they do not support the hypothesis that men should always apologize. Instead, the findings suggest that men should hardly apologize at all, as Schumann and Ross (2010) suggest that women apologize more often than men.
However, one of my Hindu friends resolved the problem for me using his cultural views on gender psychology. He suggested that the rewards for men and women will never be the same due to the difference in needs. The general idea is that women always need to feel protected, while men always need to be the leaders in the relationship. If the girlfriend apologizes, she will feel unprotected regardless of what the boyfriend does. At the same time, if the girlfriend apologizes and the boyfriend does not, he will lose the sense of leadership, while if the boyfriend apologizes and the girlfriend does not, he will gain the sense of leadership. In this case, the reward matrix would look different (see Table 4).
In this payoff matrix, both players have a dominant strategy. The boyfriend should always apologize, as the outcomes are always better in this scenario, regardless of what the girlfriend does. At the same time, the girlfriend should always wait for an apology for the same reason. In summary, from the point of view of Hindu culture, as explained by my friend, women should let their men have a chance to apologize to feel as leaders in the relationship.
Before concluding the story, I wanted to mention that my Hindu friend does not always apologize first, as after 10-20 fights, the feeling of being used kicks in, which affects the payoff matrix drastically.
Example 3: The Hang-Up Problem
Movies often depict these stories the stories where a loving couple cannot decide which person should hang up the phone. While it may seem cute, my male friend says that it is unbearable to be in the situation. Before jumping to the discussion about my friend’s idea of the situation, it is beneficial to look at the problem using the game theory.
The reason why the game even starts is that both people see much value in continuing the conversation on the phone even when they run out of things to talk about. This value is always greater than the value of hanging up the phone, which puts the boyfriend and the girlfriend in a vicious cycle of saying, “No, you hang up!” The only constraint of the game is the time both players have to spare before they are obliged to devote their time to actual duties. The game assumes that the value of hanging up is 0, and the value of continuing the conversation is 45 for the boyfriend and 55 for the girlfriend. The benefits are defined by the amount of time each player has left. It is also assumed that the cost of the round is 10, which implied that the benefits decrease each round by this amount. Thus, the person to hang up first is the one who runs out of time first, which will be demonstrated that his payoff will become negative, which is below the value of hanging up.
While this explanation appears rational, my friend said that it was not the situation he had had with his ex-girlfriend. The inability to solve the problem contributed to them breaking up. The situation with the hang-up game can be modeled as the classic game of the war of attrition. The problem was that the girlfriend would always get mad if my friend hung up first. At the same time, his girlfriend believed that if she hung up first, my friend would get mad. The game is modeled in Figure 1 below. The game assumes that the “reward” of hanging up is -100, while the value of waiting is zero. The cost of the round is 10. In the case that the decision for the fifth round is to wait, the winner is randomly selected with expected payoff of -75, as both players become frustrated with the game wasting their time. Additionally, whoever hangs up first will need to suffer from their partner being mad.
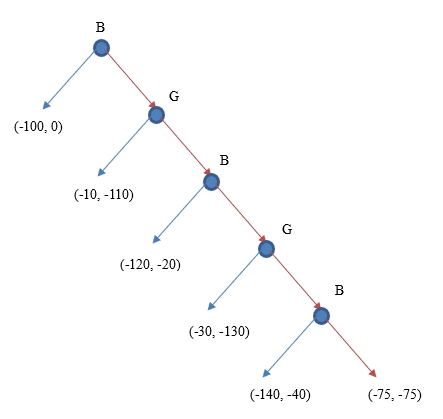
Backward induction demonstrates that the SPNE at every decision node is to wait rather than hang up the phone. However, the continuation of the conversation leads to deterioration of the situation, which makes it even harder to incline towards stopping the conversation. The best decision in this game, holding that all the assumptions remain the same, would be to flip a coin and the beginning of the game. Then the expected payoff would be -50 for both players. However, flipping the coin appears impossible in this situation. Additionally, even if one player would be decided to hang up the phone first, it is very likely that he or she would decide to wait instead.
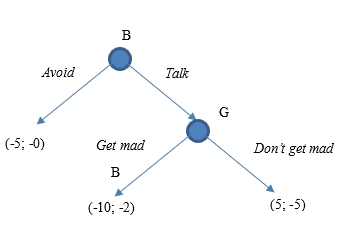
In reality, playing the game was actually a wrong decision in the beginning, as the best outcome for any player is 0 in benefits (assuming the first player decides to hang up). The best decision would be to talk about the problem and come with a reasonable solution. When I asked my friend why he did not talk to his girlfriend about the problem, he said that it was impossible to talk to her as she would get mad. While I did not have any arguments to explain why he needed to talk to his girlfriend when he had a chance, I have some rational explanations for the matter now, as I learned game theory. The game my friend thinks of would look like the one in Figure 2 below. My friend believed that if he selected not to talk, he would feel bad, and his girlfriend would be indifferent. At the same time, if he decided to talk, backward induction demonstrates that his girlfriend would always select to get mad, which would aggravate the situation even further. Thus, it would always be better to avoid the conversation.
I believe that there were certain flaws to the assumptions used by my friend. First, we all now know that avoiding the conversation would lead to them breaking up, which means that the benefits for both parties would look different. In fact, the situation of avoiding the talking is equally bad for both parties. Second, the game does not end at the girl getting or not getting mad. In reality, if the girl gets mad, the boyfriend always has a chance to apologize. Thus, I believe that the game of talking over the problem would look like the one demonstrated in Figure 3 below.
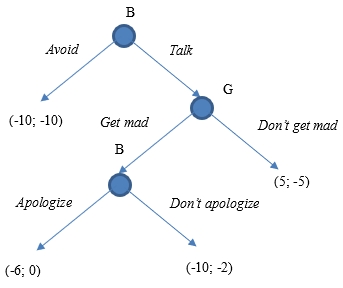
Backward induction demonstrates that the best scenario in this game is Talk → Get mad→ Apologize. Additionally, it should be acknowledged that the purpose of the game is to talk about the problem to try and solve it. If the girlfriend gets mad, it may still be acceptable if there is a chance that she understands that there is a hanging-up problem and tries to solve it.
Example 4: Setting the Price
As shown in the first three examples, game theory can be helpful for solving relationship problems and everyday situations. However, it is also frequently used in business. Recently, I was able to explain the pricing strategy of the bakery in which I work, using game theory. In particular, modeling the situation using the game theory helped me understand why our bakery sets a high price on its products instead of setting a low price to attract more customers.
Our baker operates in a small town, where only two bakeries exist. The other bakery is across the road from us, and the prices in the bakery are always lower than ours. For instance, the most popular product, cinnamon buns, costs around $6, while the cost of the bun is $3.99 at the bakery across the road. I always believed that by setting a lower price, our bakery can attract more customers and make more profit by increase the sales and decreasing the profit margin. When I asked my boss why we never set a low price for cinnamon buns, he replied that we would never be able to beat the price of the baker across the road.
The problem was that the baker across the road was a part of a bakery chain with hundreds of locations around the state. This implied that our competitors could use economies of scale to decrease the cost of every single product, as they could buy ingredients in bigger batches. The suppliers also set lower prices for them on raw materials, as our competitors had higher bargaining power. The managing and the accounting costs per product sold were also lower, which enabled them to have low prices on their products. If we tried to match their prices, we would have needed cheaper ingredients, which would make the quality of our products deteriorate. This was against the principles of our bakery. Our mission is to combine high-quality ingredients and extraordinary taste to provide our customers with the best baking products in the area. As we did were unable to match our competitor’s prices, we would not have attracted many customers by lowering the prices, as those who wanted a good bargain would still go to the bakery across the road.
The price selection strategy can be explained using the reward matrix provided in Table 5 below.
The reward matrix demonstrates that if our competitors decided to set a high price, we would prefer setting a lower price, as the payoffs are higher. At the same time, if our competitors decided to set a low price, we would prefer to set a high price. In other words, we do not have a dominant strategy. Our competitors, however, do have a dominant strategy. Our competitors are better off setting low prices regardless of what pricing strategy our bakery selected. Thus, the top right quadrant of the reward matrix is the Nash Equilibrium of the game. This implies that our bakery will not change its decision unless our competitors change their strategy. However, the competitors will not change their decision regardless of what we do. As luck would have it, it is almost the quadrant that has the highest payoff for our competitors, which makes the owner of our company jealous. However, since he is a rational man, he will not change his decision.
After describing the game demonstrated above, I decided that the rules were overly simplified. In reality, I believe that there are more than just two strategies of having low price or high price. So, decided to speculate what would happen if it was a three-strategy two-player game. The reward matrix for the game is provided in Table 6 below. I decided to leave the payoffs for the four combinations of strategy the same and speculated what would happen if a medium-price strategy was added to the analysis.
The game described above is similar to the one demonstrated in Table 5. While our bakery does not have a dominant strategy, the competitors have a clear dominant strategy, which is to keep the prices low. In other words, the competitors should use their advantage of the economies of scale and sell similar products at the lowest possible price. Our bakery, however, is forced to have high prices on our products, which limits our revenues. However, the Nash equilibrium from the games described above helps to select the marketing strategy.
Example 5: Buying My First Car
When I turned sixteen, my father told me that it was time for me to have a car of my own. This was the time I dreamt about for two years. At that point, I went through thousands of offers in local newspapers, eBay, and local dealerships. I knew that my first car was going to be a used one, and I was prepared for that. However, what I was not prepared for is to drive my father’s car. I always knew it was a possibility, as my father also wanted to buy a new car at that point. So, it was rational for him to give me his old car, as it was rational for him. At the same time, he wanted me to have the brand of car I wanted, as he took selecting the brand of car seriously and believed that everyone should be loyal to the brand of car they select.
At that point, I wanted to have a Chevy or a Nissan, with Chevy being my priority. There were two problems associated with the selected brands. On the one hand, if I told my father that I wanted to have a Chevy, he would give me his old Chevy. On the other hand, if I told my father that I wanted a Nissan, he would not give me much money, as he believed that American cars are the best. So, my best option was to ask for a Ford, as my father was ready to give me $8,000, which was an enormous amount of money for our family at the time. However, I was uncertain whether my father would give me less money if I selected Nissan. I also was not sure if he would decide to give me his Chevy if I opted for a Chevy. In my head, the game looked like the one depicted in Figure 4 below.
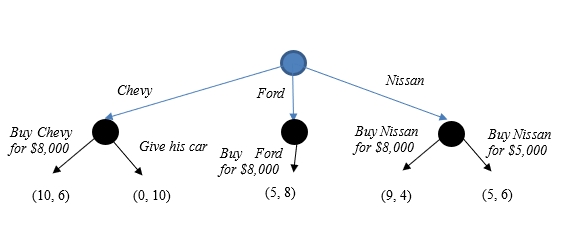
The game provided above explains why I was at a loss. Backward induction demonstrates that I should have randomized between selecting Ford and Nissan, as these two options would bring me the same benefits. If I were a good kid and wanted to make my father happy, I should have selected Ford over Nissan, as it would be more pleasing for my father and indifferent for me. In reality, selected Nissan but not because I was a bad kid. I realized that the game of buying a new car was actually a three-player game. Before encountering the dilemma, I had not realized that my mother was also a stakeholder in the game.
My mother always preferred safety over anything else. She believed that me having my father’s car would be the best option. However, she always wanted to make me feel good and make a choice for myself. This implied that she could overrule my father’s decision by talking to him, but she would not overrule my decision. Thus, before making the decision, I told my mother that I was inclined to buy a Ford if my father would not let me buy a Nissan for $8,000. My mother hated Ford, as she believed it was the most unreliable car on Earth. At the same time, she believed that Nissan was a very safe choice. This turned the game into the three-player two-strategy sequential game demonstrated in Figure 5 below.
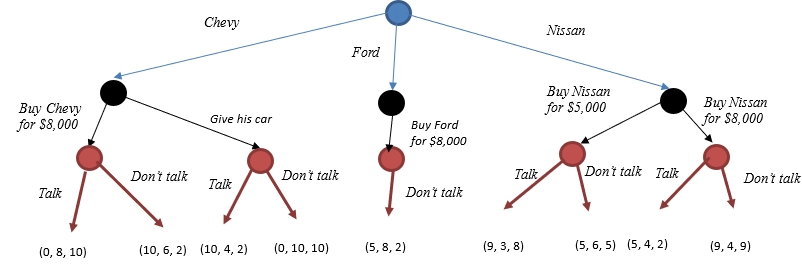
This game can be solved using backward induction. It is clear that my mother would not overrule my father’s decision to give me his car, and she would overrule if he decided to buy me a Chevy for $8,000. At the same time, she would choose to overrule my father’s decision to buy a Nissan for $5,000. This game demonstrates how my father did not really have a choice. The only choice he could make was whether he wanted to be overruled or not. I think that it is a very fair representation of reality.
Conclusion
This paper demonstrated that game theory can be used in a wide variety of situations. Learning this theory helped me explain my actions in the past, such as betraying my cousin and manipulating my father’s decision about buying my first car. Game theory also helped me explain the hang-up dilemma and prove the notion that men should always apologize. The most crucial takeaway from this theory, however, was the ability to explain the marketing and the pricing strategy of the bakery I work in. I will try to use the theory in the future to make business and life decisions.
References
Harrington, J. (2015). Games, strategies, and decision making (2nd ed.). Worth Publishers.
Schumann, K., & Ross, M. (2010). Why women apologize more than men: Gender differences in thresholds for perceiving offensive behavior. Psychological Science, 21(11), 1649-1655. Web.
